深度学习入门_P3 神经网络的学习

1. 从数据中学习

前面权重和偏置都是我们手动去指定的，如果神经网络中所有的参数都需要我们手动去指定这个工作量非常大，而神经网络的特征则是从数据中学习，可以根据数据自动决定权重参数的值。
机器学习的方法极力避免人为介入，尝试从收集到的数据中发现答案。
计算机视觉领域，常用的特征量包括 SIFT，SURF和HOG 等。使用这些特征量将图像转换为向量，然后对转换后的向量使用机器学习中的 SVM，KNN 等分类器进行学习。

输入 -> 人想到的算法 -> 答案
输入 -> 人想到的特征量 -> 机器学习 -> 答案
输入 -> 神经网络 -> 答案

1.1. 训练数据和测试数据

一般将数据分为训练数据和测试数据两部分来进行学习和实验。
为了正确评估模型的泛化能力，就必须划分为训练数据和测试数据，另外，训练数据也可以称为监督数据。
只对某个数据集过度拟合的状态称为过拟合，避免过拟合也是机器学习的一个重要课题。

2. 损失函数

神经网络以某个指标为线索寻找最优权重的参数，叫做损失函数。

2.1. 均方误差

可以用作损失函数的函数有很多，其中最有名的是均方误差。

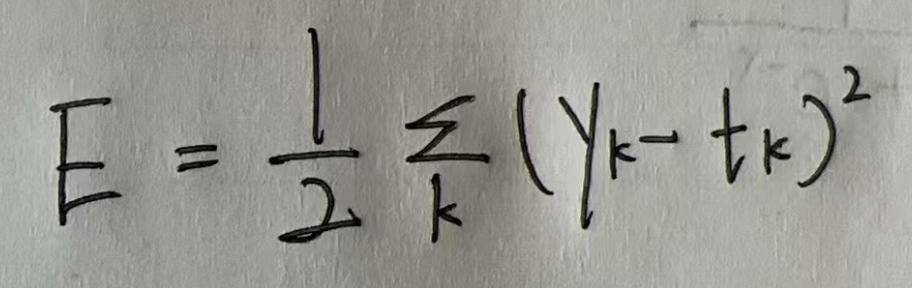
y_k 表示神经网络的输出，t_k 表示监督数据。

import numpy as np

def mean_squared_error(y, t):
    return 0.5 * np.sum((y - t) ** 2)

# 测试，0-9的手写数字识别，正确答案是2，预测答案是0.6
t1 = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
y1 = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]

# 正确答案是2，预测答案是0.1，误差很大
t2 = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
y2 = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]

print(mean_squared_error(np.array(y1), np.array(t1)))  # 0.09750000000000003
print(mean_squared_error(np.array(y2), np.array(t2)))  # 0.5975000000000001

可以看到如果神经网络的预测错了会导致均方误差很大。

2.2. 交叉熵误差

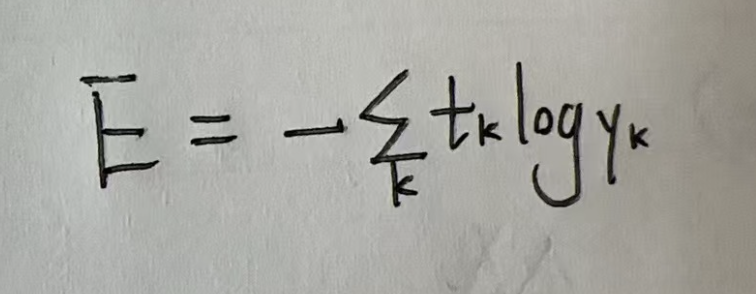
def cross_entropy_error(y, t):
    delta = 1e-7
    return -np.sum(t * np.log(y + delta))

# 测试
print(cross_entropy_error(np.array(y1), np.array(t1)))  # 0.5108254570958627
print(cross_entropy_error(np.array(y2), np.array(t2)))  # 2.3025850929940455

2.3. mini-batch 学习

前面说的所有误差都是针对单个数据而言，如果训练数据有 100 条，这个时候需要对这 100 条数据的误差加起来再除以 100 进行正规化。
如果训练数据过大有几百万，几千万条这个时候如果对所有数据误差计算是不可能的，这个时候需要随机从中间抽取部分数据进行学习，这种方式叫做 mini-batch 学习。

(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()

train_size = x_train.shape[0]
batch_size = 10
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
y_batch = y_train[batch_mask]

从 mnist 数据集中随机选择 10 个数据作为训练集。

2.4. 为何要定义损失函数

损失函数可以用来对神经网络中的权重进行调整，通过对该权重的损失函数进行求导可以知道增加或者减少权重对损失函数值的影响。

3. 数值微分

3.1. 导数

Python 中差分不能无限小，过小的数值会产生舍入误差，将数字控制在 10^-4 即可。

print(np.float32(1e-50))  # 0.0

利用差分求导本身就具备误差，因为 f(x+h) - f(x)/h 中 h 的数值不可能做到无限小。为了减小这种误差可以使用中心差分 f(x+h) - f(x-h)/2h 。
利用微小差分求导的过程称之为数值微分。而通过数学推导求导的过程称为解析性求解，或者解析性求导。

def numerical_diff(f, x):
    h = 1e-4
    return (f(x + h) - f(x - h)) / (2 * h)

3.2. 偏导数

有多个变量的函数的导数称为偏导数。

假设有一个函数是 f(x0, x1)=x0**2 + x1**2 针对这个函数求偏导数。

# x0 = 3, x1 = 4 偏导数
def function_tmp1(x0):
    return x0**2 + 4**2

# x0 = 3, x1 = 4 偏导数
def function_tmp2(x1):
    return 3**2 + x1 ** 2

print(numerical_diff(function_tmp1, 3))  # 6.00000000000378
print(numerical_diff(function_tmp2, 4))  # 7.999999999999119

3.3. 梯度

如上所示，由 (x0, x1) 的偏导数组成的向量就成为值 梯度。
梯度指向各点处函数值下降最多的方向。